(ST2) Integral Test#

In this lesson we are going to see how to:

  • use the Integral Test to show that a series is either convergent or divergent.

Review Video#

The Test#

Integral Test

Suppose \(a_n\) is a sequence such that \(a_n=f(n)\) where \(f\) is a continuous, positive, decreasing function on the interval \([1,\infty)\).

If \(\displaystyle \int_1^{\infty} f(x)\, dx\) is convergent, then \(\displaystyle \sum_{n=1}^{\infty} a_n \) is convergent.

If \(\displaystyle \int_1^{\infty} f(x)\, dx\) is divergent, then \(\displaystyle \sum_{n=1}^{\infty} a_n \) is divergent.

Necessary Conditions#

To use the Integral Test, (before we actually compute the improper integral) we first need to check that the function:

  1. \(f\) is continuous.

  2. \(f\) is positive.

  3. \(f\) is decreasing.

How do we check decreasing? There are a few ways we can show this: either directly using inequalities or by looking at the sign of the derivative.

  1. Inequality Definition: \(f\) is decreasing if \(x_1< x_2\) implies \(f(x_1) > f(x_2)\).

  2. Derivatives: \(f\) is decreasing if \(f'\) is negative.

Warning#

Warning

One common mistake with the Integral Test is to claim that the sum of the series is equal to the value of the improper integral. In general,

\[ \sum_{n=1}^{\infty} a_n \neq \int_{1}^{\infty}f(x)\, dx \]

Intuitive Proof#

The idea behind this test is that we can think of our series and more specifically the sequence of partial sums as representing the rectangular approximation of the area under the curve.

Convergent

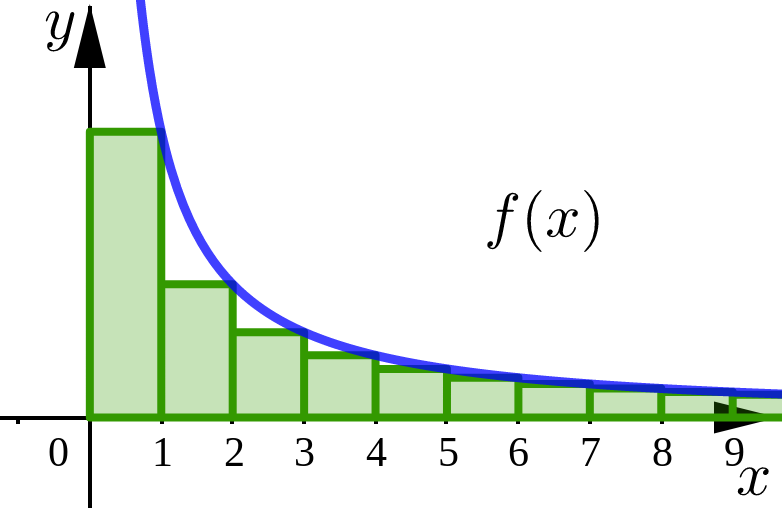
convergence

  • Right endpoint rectangles.

  • The conditions on \(f\) help ensure that each right rectangle is under the curve.

  • Since the improper integral is convergent, the exact area under the curve is finite.

Divergent

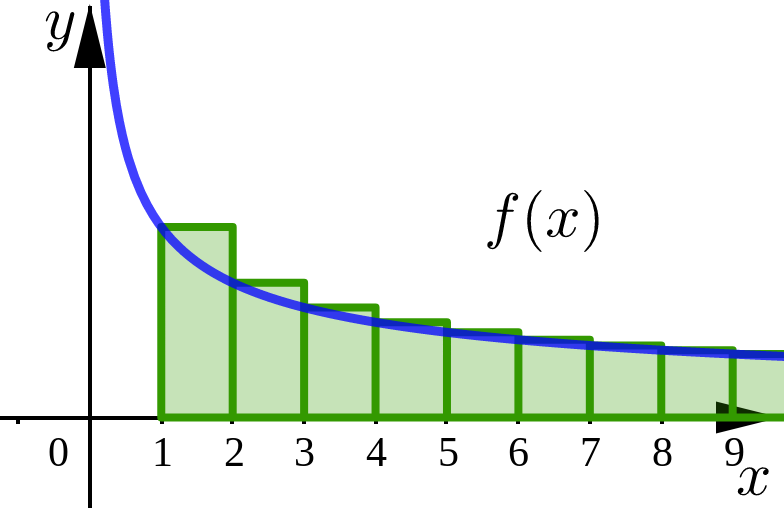
divergence

  • Left endpoint rectangles.

  • The conditions on \(f\) help ensure that each left rectangle is above the curve.

  • Since the improper integral is divergent, the exact area under the curve is infinite.

Example 1#

Use the integral test to determine if the series is convergent or divergent.

\[ \sum_{n=1}^{\infty} \dfrac{1}{n^2} \]

(Click to see the steps.)

Use the function \(f(x)=\dfrac{1}{x^2}\). (Replace each \(n\)-term with an \(x\).)

  • \(f\) is continuous on \([1,\infty)\) since this is a rational function and the denominator does not equal \(0\) on the interval.

  • \(f\) is positive on \([1,\infty)\) since all terms are positive and there is no subtraction.

  • \(f\) is decreasing on \([1,\infty)\) which we show below:

Suppose \(x_1\) and \(x_2\) are two real numbers such that \(1\leq x_1 < x_2\). Then

\[\begin{split} x_1 &< x_2 \\[10pt] x_1^2 &< x_2^2 \\[10pt] \tfrac{1}{x_1^2} &> \tfrac{1}{x_2^2} \\[10pt] f(x_1) & > f(x_2) \end{split}\]
\[\begin{split} \int_1^{\infty} \dfrac{1}{x^2} \, dx & = \lim_{b\to \infty} \int_1^{b} \dfrac{1}{x^2} \, dx \\[10pt] & = \lim_{b\to \infty} -x^{-1} \biggr|_1^{b} \\[10pt] & = \lim_{b\to \infty} 1-\dfrac{1}{b} \\[10pt] & = 1-0 \\[10pt] & =1 \\[10pt] \end{split}\]

Since the improper integral converges, we conclude that our series converges as well by the Integral Test.

Sum? Even though \( \displaystyle \int_1^{\infty} \dfrac{1}{x^2} \, dx = 1\), we cannot say that the sum of the series is 1. In fact:

\[ \sum_{n=1}^{\infty} \dfrac{1}{n^2} =\dfrac{\pi^2}{6}\neq 1 \]

Starting Index Value#

Tip

As usual, we can relax the starting index value to include other values besides \(n=1\), and the Integral Test still applies.

Also, we can relax the condition that function \(f\) is continuous, positive, decreasing function on the interval \([1,\infty)\). It just needs to eventually satisfy these conditions on some interval \([N,\infty)\).

In the case of a discontinuity we could use \(\displaystyle \int_N^{\infty} f(x)\, dx\) to determine whether \(\displaystyle \sum_{n=N}^{\infty} a_n \) is convergent or divergent.

Tail of a Series

The series \(\displaystyle \sum_{n=N}^{\infty} a_n \) is convergent if and only if \(\displaystyle \sum_{n=1}^{\infty} a_n \) is convergent.

Example 2#

Determine if the following series is convergent or divergent.

\[ \sum_{n=1}^{\infty} \dfrac{\ln n}{n} \]

(Click to see the steps.)

Use the function \(f(x)=\dfrac{\ln x}{x}\). (Replace each \(n\)-term with an \(x\).)

  • \(f\) is continuous on \([1,\infty)\) since this is a rational function and the denominator does not equal \(0\) on the interval.

  • \(f\) is positive on \([2,\infty)\) since all terms are positive and there is no subtraction.

  • \(f\) is decreasing on \([3,\infty)\) which we show below using the derivative:

\[\begin{split} f'(x) = \dfrac{1-\ln x}{x^2} &<0 \\[10pt] 1- \ln x & <0 \\[10pt] 1 & < \ln x \\[10pt] e^1 & < e^{\ln x} \\[10pt] e & < x \\[10pt] \end{split}\]
\[\begin{split} \int_1^{\infty} \dfrac{\ln x}{x} \, dx & = \lim_{b\to \infty} \int_1^{b} \dfrac{\ln x}{x} \, dx \\[10pt] & = \lim_{b\to \infty} \tfrac{1}{2} \left(\ln x\right)^2 \biggr|_1^{b} \\[10pt] & = \lim_{b\to \infty} \tfrac{1}{2} \left(\ln b\right)^2 - \tfrac{1}{2} \left(\ln 1\right)^2\\[10pt] & = \lim_{b\to \infty} \tfrac{1}{2} \left(\ln b\right)^2 \\[10pt] & = \infty \\[10pt] \end{split}\]

Since the improper integral diverges, we conclude that our series diverges as well by the Integral Test.

Example 3#

Determine if the following series is convergent or divergent.

\[ \sum_{n=2}^{\infty} \dfrac{1}{n^2+4} \]

(Click to see the steps.)

Use the function \(f(x)=\dfrac{1}{x^2+4}\). (Replace each \(n\)-term with an \(x\).)

  • \(f\) is continuous on \([2,\infty)\) since this is a rational function and the denominator does not equal \(0\) on the interval.

  • \(f\) is positive on \([2,\infty)\) since all terms are positive and there is no subtraction.

  • \(f\) is decreasing on \([2,\infty)\) which we show below using the derivative:

\[ f'(x) = \dfrac{-2x}{(x^2+4)^2} \]

Since the denominator is always positive, we see that the derivative is negative when the numerator is less than 0.

\[\begin{split} f'(x) = \dfrac{-2x}{(x^2+4)^2} &<0 \\[10pt] -2x & <0 \\[10pt] 0 & < 2x \\[10pt] 0 & < x \\[10pt] \end{split}\]

Therefore \(f'\) is negative on our desired interval \([2,\infty)\).

\[\begin{split} \int_2^{\infty} \dfrac{1}{x^2+4} \, dx & = \lim_{b\to \infty} \int_2^{b} \dfrac{1}{x^2+4} \, dx \\[10pt] & = \lim_{b\to \infty} \tfrac{1}{2} \tan^{-1}\left(\tfrac{x}{2}\right) \biggr|_2^{b} \\[10pt] & = \lim_{b\to \infty} \tfrac{1}{2} \tan^{-1}\left(\tfrac{b}{2}\right) - \tfrac{1}{2} \tan^{-1}\left(\tfrac{2}{2}\right) \\[10pt] & = \lim_{b\to \infty} \left(\tfrac{1}{2} \tan^{-1}\left(\tfrac{b}{2}\right) - \tfrac{1}{2}\cdot \tfrac{\pi}{4} \right)\\[10pt] & = \tfrac{\pi}{2} - \tfrac{1}{2}\cdot \tfrac{\pi}{4}\\[10pt] & = \tfrac{3\pi}{8} \\[10pt] \end{split}\]

Since the improper integral converges, we conclude that our series donverges as well by the Integral Test.