(PE1) Parametric Equations#

By the end of the lesson you will be able to:

  • graph a parametric curve by plotting individual points.

  • use an arrow to indicate the direction the curve is traced out as parameter \(t\) increases.

Review Videos#

Curves in the Plane#

How can we describe a curve in the plane?

Parametric Curve

Suppose that \(x\) and \(y\) are both functions of a third variable \(t\)

\[ x=f(t)\qquad \qquad y=g(t) \]

We call such equations parametric equations.

As \(t\) varies, the point \(\big(x,y\big)=\big(f(t),g(t)\big)\) varies and traces out a curve, which we call a parametric curve.

A few things to note about parametric equations:

  • We normally think of variable \(t\) as representing time.

  • Think of the point \((x,y)\) as the position of a particle at time \(t\).

  • Variables \(x\) and \(y\) are no longer directly related to each other.

Example 1#

Sketch the curve with parametric equations:

\[ x=t^2-2t\qquad \qquad y=t+1 \]

parametric1

Example 2#

Sketch the curve with parametric equations:

\[ x=t^2-2t\qquad \qquad y=t+1 \]

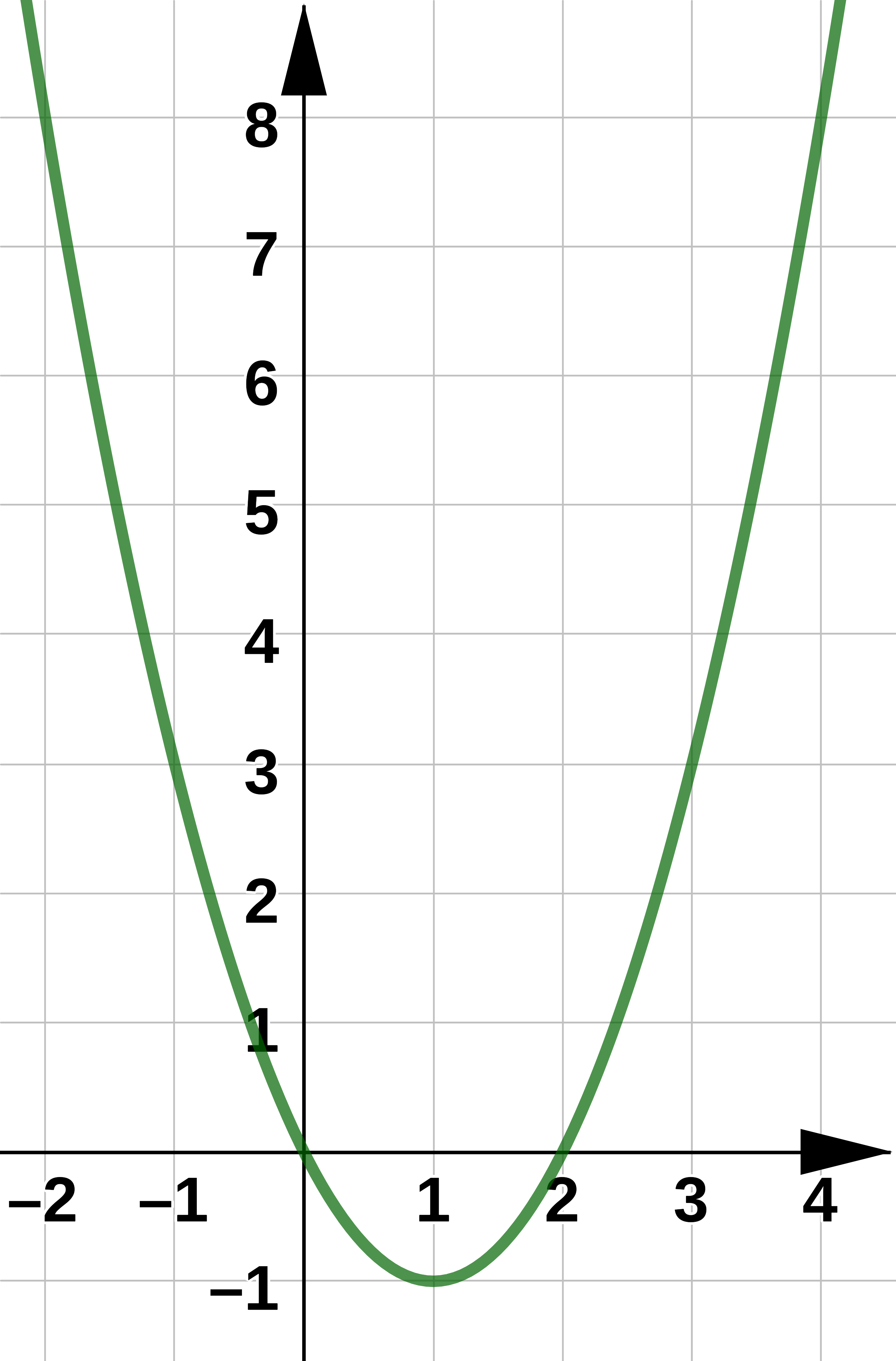
parametric2a

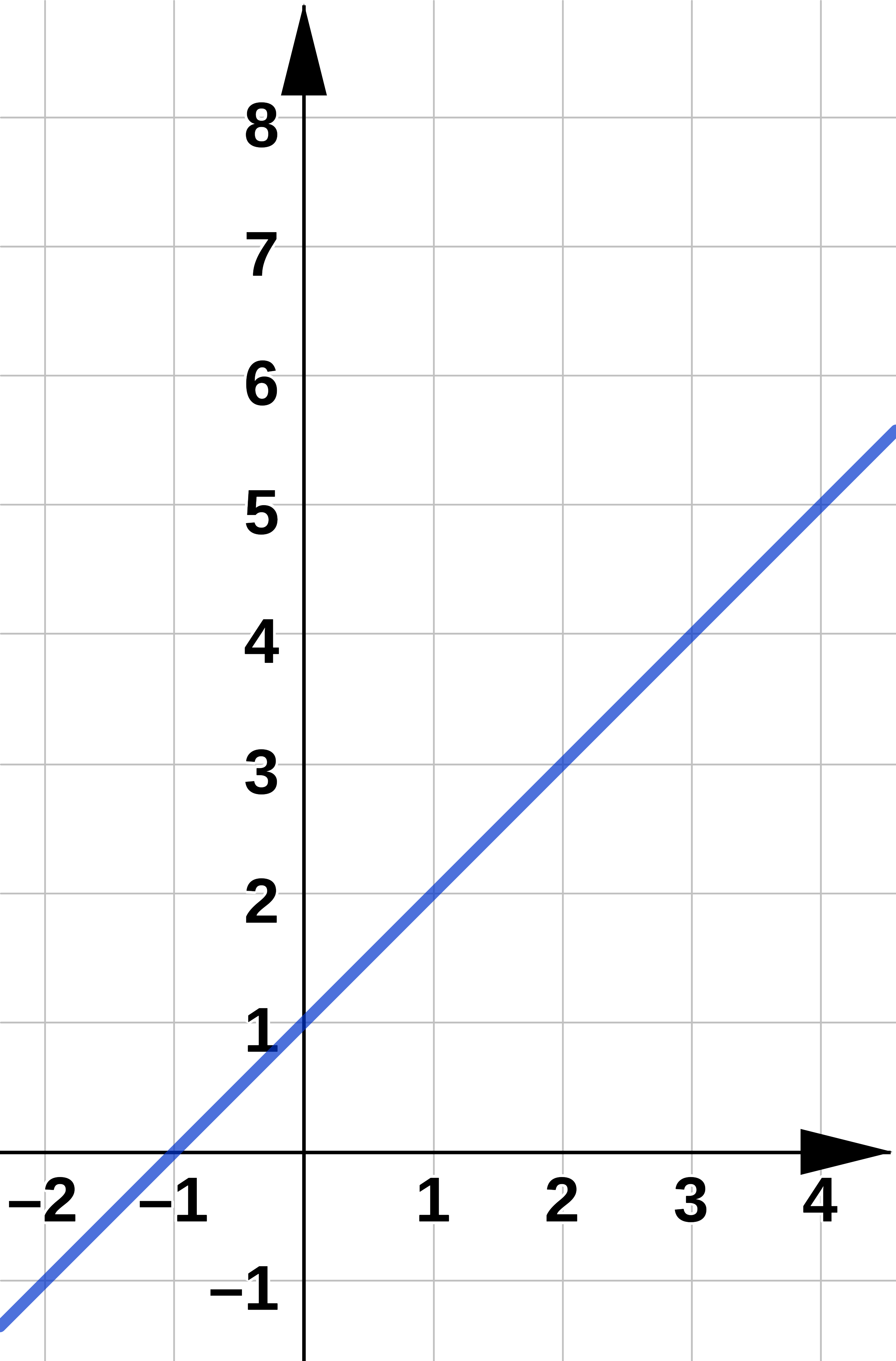
parametric2b

Example 2#

Sketch the curve with parametric equations:

\[ x=t^2-2t\qquad y=t+1 \quad \text{with} \quad 0\leq t\leq 4 \]

parametric1