(AD2) Volume of a Solid of Revolution#

In this lesson we are going to see how to:

  • calculate the volume of a solid obtained by rotating a region of the \(xy\)-plane around a fixed axis.

Review Videos#

No review videos for this lesson.

Solid of Revolution#

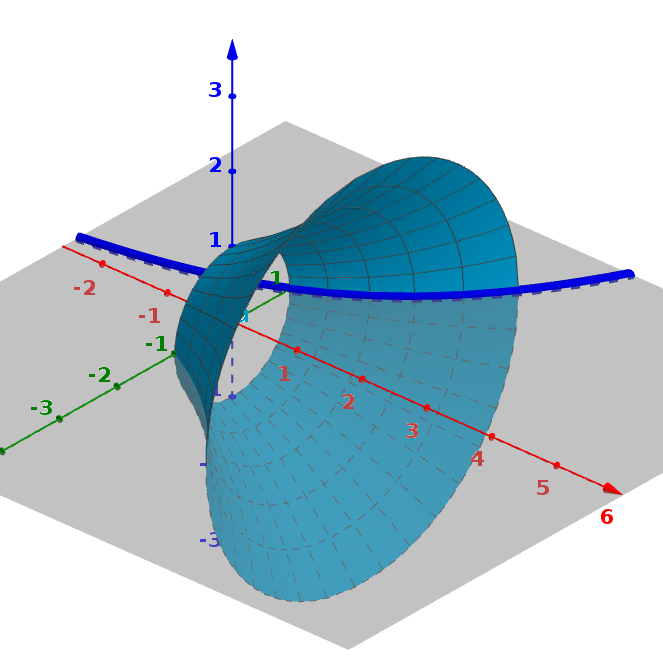
We obtain a solid of revolution by taking a region of the \(xy\)-plane, a line (which we call the axis of rotation), and then rotating the region around this specified axis.

For example:

Planar Region

volume2

Three Dimensional Object

volume1

Integral Formula#

Volume of a Solid of Revolution

The volume of the solid from \(x=a\) to \(x=b\) is given by:

\[ \text{Volume }= \int_a^b A(x) \, dx \]

where \(A(x)\) represents the area of the cross-sectional cut perpendicular to the \(x\)-axis.

Example 1#

Find the volume of the solid obtained by revolving the given region about the \(x\)-axis.

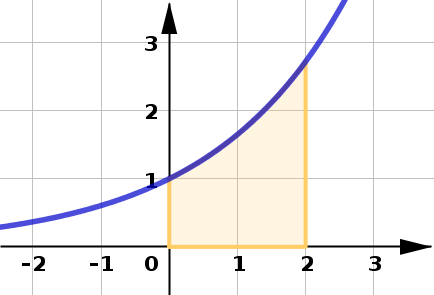
  • Region below by \(y=e^{x/2}\) from \(x=0\) to \(x=2\)

volume2

Example 2#

Find the volume of the solid obtained by revolving the given region about the \(y\)-axis.

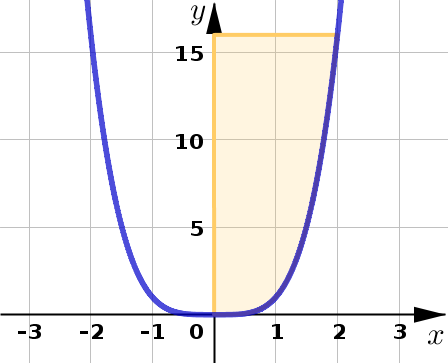
  • Region bounded by \(y=x^4\), \(y=16\), and \(x=0\).

volume3

Example 3#

Find the volume of the solid obtained by revolving the given region about the \(x\)-axis.

  • Region bounded by \(y=x^2-6x+10\) and \(y+2x=7\).

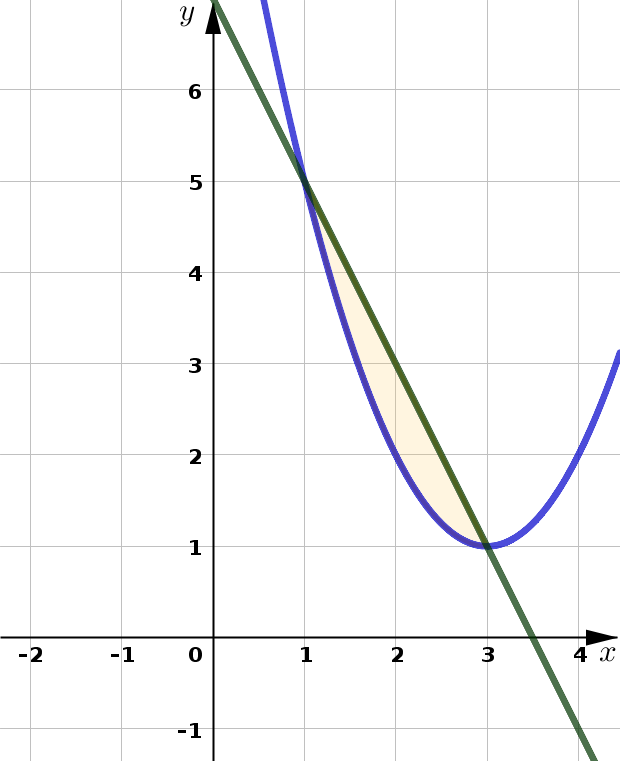
volume4

Example 4#

Set up, but do not evaluate, the integral which gives the volume for the solid obtained by rotating the given region about the line \(y=-1\)

  • Region bounded by \(y=x^2-6x+10\) and \(y+2x=7\).

volume4

Example 5#

Set up, but do not evaluate, the integral which gives the volume for the solid obtained by rotating the given region about the line \(y=6\)

  • Region bounded by \(y=x^2-6x+10\) and \(y+2x=7\).

volume4

Example 6#

Set up, but do not evaluate, the integral which gives the volume for the solid obtained by rotating the given region about the line \(x=-2\)

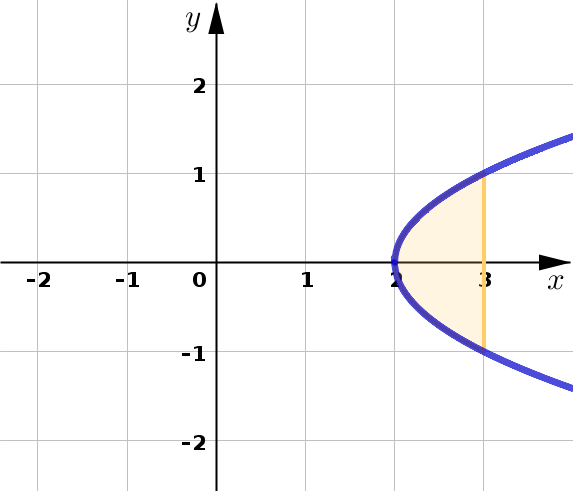
  • Region bounded by \(x-y^2=2\) and \(x=3\).

volume5