(S1) Sequences#

In this lesson we are going to introduce the definition of a sequence, look at the different types of notation, and see how to visualize a sequence graphically.

By the end of this lesson, you will be able to:

  • write out the first few terms of a sequence given the general term \(a_n\).

Review Videos#

Definition of a Sequence#

Sequence

A sequence is a function with the set of positive integers as its domain.

We tend to think of a sequence as an infinite list:

\[ \bigg\{a_1, \; a_2, \; a_3, \, \dots , \, a_n, \, \dots\bigg\} \]

where all of the terms of the sequence are written in a specific order. Relating this to function notation, we could also say \(f(n)=a_n\). Where the \(n\)th term of our sequence is equal to the function evaluated at number \(n\).

Notation#

We usually describe a sequence with a few different notations:

Writing out the first few terms:

\[ \bigg\{a_1, a_2, a_3, \dots \bigg\} \]

Writing out the formula for the \(n\)th general term:

\[\bigg\{a_n \bigg\}_{n=1}^{\infty}\]

Example 1#

List the first four terms of the sequence:

\[\left\{ \dfrac{3n}{2n-1}\right\}_{n=1}^{\infty}\]

(Click to see the steps.)

We notice that the \(n\)-values start with \(n=1\). To find the first four terms of the sequence, we will plug \(n=1\), \(n=2\), \(n=3\), and \(n=4\) into the formula of the general term:

\[ a_n=\dfrac{3n}{2n-1} \]

Let’s calculate these:

\[\begin{split} n=1 & \quad \longrightarrow \quad & \dfrac{3(1)}{2(1)-1} = \dfrac{3}{1} = 3\\[10pt] n=2 & \quad \longrightarrow \quad & \dfrac{3(2)}{2(2)-1} = \dfrac{6}{3} = 2\\[10pt] n=3 & \quad \longrightarrow \quad & \dfrac{3(3)}{2(3)-1} = \dfrac{9}{5} \\[10pt] n=4 & \quad \longrightarrow \quad & \dfrac{3(4)}{2(4)-1} = \dfrac{12}{7}\\[10pt] \end{split}\]

Finally we write out the first four terms of our sequence:

\[ \bigg\{ 3, 2, \tfrac{9}{5}, \tfrac{12}{7} , \dots \bigg\} \]

Starting Index Value#

Starting Index Value

We can generalize the idea of sequences so that our index \(n\) starts at values other than \(n=1\).

Example 2#

List the first four terms of the sequence:

\[\bigg\{ (-1)^n (n+1) \bigg\}_{n=3}^{\infty}\]

(Click to see the steps.)

We notice that the \(n\)-values start with \(n=3\). To find the first four terms of the sequence, we will plug \(n=3\), \(n=4\), \(n=5\), and \(n=6\) into the formula of the general term:

\[ a_n=(-1)^n (n+1) \]

Let’s calculate these:

\[\begin{split} n=3 & \quad \longrightarrow \quad & (-1)^3 (3+1) = -4\\[10pt] n=4 & \quad \longrightarrow \quad & (-1)^4 (4+1) = 5\\[10pt] n=5 & \quad \longrightarrow \quad & (-1)^5 (5+1) = -6 \\[10pt] n=6 & \quad \longrightarrow \quad & (-1)^6 (6+1) = 7\\[10pt] \end{split}\]

Finally we write out the first four terms of our sequence:

\[ \bigg\{ -4, 5, -6, 7 , \dots \bigg\} \]

Factorials

\[ n! = n\cdot(n-1)\cdot \cdots \cdot 3\cdot 2 \cdot 1 \]

Example 3#

List the first four terms of the sequence:

\[\bigg\{ \dfrac{2^n}{n!} \bigg\}_{n=0}^{\infty}\]

(Click to see the steps.)

We notice that the \(n\)-values start with \(n=0\). To find the first four terms of the sequence, we will plug \(n=0\), \(n=1\), \(n=2\), and \(n=3\) into the formula of the general term:

\[ a_n=\dfrac{2^n}{n!} \]

Let’s calculate these:

\[\begin{split} n=0 & \quad \longrightarrow \quad & \dfrac{2^0}{0!} = 1\\[10pt] n=1 & \quad \longrightarrow \quad & \dfrac{2^1}{1!} = 2\\[10pt] n=2 & \quad \longrightarrow \quad & \dfrac{2^2}{2!} = 2\\[10pt] n=3 & \quad \longrightarrow \quad & \dfrac{2^3}{3!} = \tfrac{4}{3}\\[10pt] \end{split}\]

Finally we write out the first four terms of our sequence:

\[ \bigg\{ 1, 2, 3, \tfrac{4}{3} , \dots \bigg\} \]

Example 4#

Find a formula for the general term \(a_n\) of the following sequence. Suppose that the sequence starts with index \(n=1\).

\[\bigg\{ -\dfrac{3}{4}, \dfrac{9}{5}, -\dfrac{27}{6}, \dfrac{81}{7} , \dots \bigg\}\]

(Click to see the steps.)

We begin by noticing the alternating \(\quad - \quad + \quad - \quad + \quad \) pattern. How do we achieve this? Usually with either:

\[ (-1)^{n-1} \quad \text{or} \quad (-1)^n \quad \text{or} \quad (-1)^{n+1} \]

Since our index starts at \(n=1\), we see that only one of these works:

\[\begin{split} &(-1)^{n-1} \quad &\longrightarrow \qquad + \quad - \quad + \quad -\\[10pt] &(-1)^{n} \quad &\longrightarrow \qquad - \quad + \quad - \quad +\\[10pt] &(-1)^{n+1} \quad &\longrightarrow \qquad + \quad - \quad + \quad -\\[10pt] \end{split}\]

So we will use \((-1)^n\) in our final answer.

Next let’s look at the numerator. And to help with this let’s write out the index number that corresponds with each term:

Index

1

2

3

4

Numerator

\(3\)

\(9\)

\(27\)

\(81\)

To make this even more useful let’s try to factor each term in the numerator:

Index

1

2

3

4

Numerator

\(3\)

\(3^2\)

\(3^4\)

\(3^4\)

We see that in the:

  • first term we have one copy of \(3\)

  • second term we have two copies of \(3\)

  • third term we have three copies of \(3\)

So we conclude that the \(n\)th term would have \(n\) multiples of \(3\) or more specifically \(3^n\).

We also want to consider the denominator. Again, let’s write out the index number that corresponds with each term:

Index

1

2

3

4

Denominator

\(4\)

\(5\)

\(6\)

\(7\)

We see that the denominator in the

  • first term is 3 more than index 1: \(\quad 4=3+1\)

  • second term is 3 more than index 2: \(\quad 5=3+2\)

  • third term is 3 more than index 3: \(\quad 6=3+3\)

So we conclude that the \(n\)th term would be 3 more than index \(n\) or more specifically: \(3+n\).

So far we have found that:

  • the \(-+-+\) pattern gives us \((-1)^n\)

  • the numerator would have \(3^n\)

  • the denominator would have \(n+3\).

Putting this all together, we get:

\[ a_n = (-1)^n\cdot \dfrac{3^n}{n+3} \]

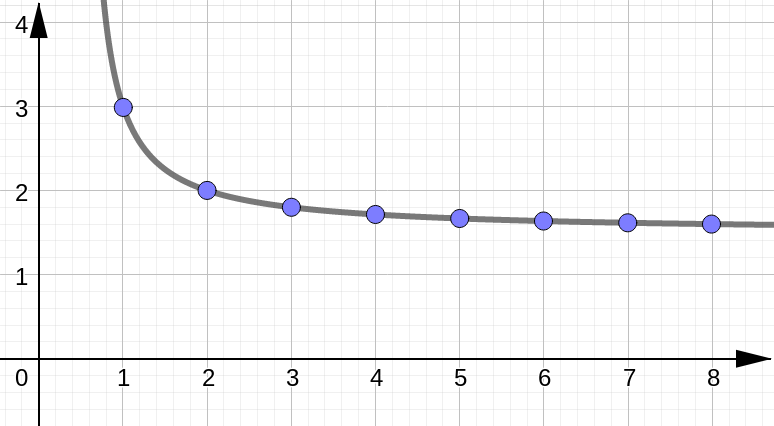
Graphical Representation#

Sometimes it helps to have a visual depiction of a sequence.

Plot on the Cartesian Plane#

Plot the points \((n,a_n)\) on the usual \(xy\)-plane:

sequence1

Plot on the Number Line#

Plot each term of the sequence \(a_n\) on the number line:

sequence2