(PS5) Taylor and Maclaurin Series#

In this lesson we are going to see:

  • how to find the Taylor and Maclaurin Series for a given function.

  • how to find the \(n\)-th degree Taylor polynomial for a given function.

Review Videos#

Definitions#

Taylor Series

Given a function \(f\), the Taylor Series of \(f\) centered at \(a\) is given by:

\[ \sum_{n=0}^{\infty}\dfrac{f^{(n)}(a)}{n!}(x-a)^n = f(a)+ \dfrac{f^{'}(a)}{1!}(x-a)+ \dfrac{f^{''}(a)}{2!}(x-a)^2 + \cdots \]

A few comments about the notation:

  • Factorial \(0!=1\)

  • \(f^{(n)}(a)\) represents the \(n\)-th derivative evaluated at \(a\).

We also have the special case of the Taylor Series where we set \(a=0\). This is called the Maclaurin Series:

Maclaurin Series

Given a function \(f\), the Maclaurin Series is given by:

\[ \sum_{n=0}^{\infty}\dfrac{f^{(n)}(0)}{n!}x^n = f(0)+ \dfrac{f^{'}(0)}{1!}x+ \dfrac{f^{''}(0)}{2!}x^2 + \cdots \]

Example 1#

Find the Maclaurin Series of the function \(f(x)=e^x\). Find the Radius of Convergence of the series.

Example 2#

Find the Taylor Series of the function \(f(x)=e^x\) centered at \(a=3\).

Power Series Representation#

Theorem

If a function has a power series representation centered at \(a\), then the function is equal to its Taylor Series at \(a\):

\[ f(x) = \sum_{n=0}^{\infty}\dfrac{f^{(n)}(a)}{n!}(x-a)^n \qquad |x-a|<R \]

Note:

  1. This theorem requires that function \(f\) has a power series representation. However, not every function has such a representation.

  2. Every function we will be considering though, does have a power series representation.

Proof#

Suppose function \(f\) has a power series representation centered at \(a\). This means:

\[ f(x) = \sum_{n=0}^{\infty}c_n(x-a)^n \]

To prove the theorem, we need to calculate the coefficients \(c_n\).

Example 3#

Find the Maclaurin Series of the function \(f(x)=\sin x\). Find the Radius of Convergence of the series.

Example 4#

Find the Taylor Series of the function \(f(x)=\dfrac{1}{1-2x}\) centered at \(a=-1\). Find the Radius of Convergence of the series.

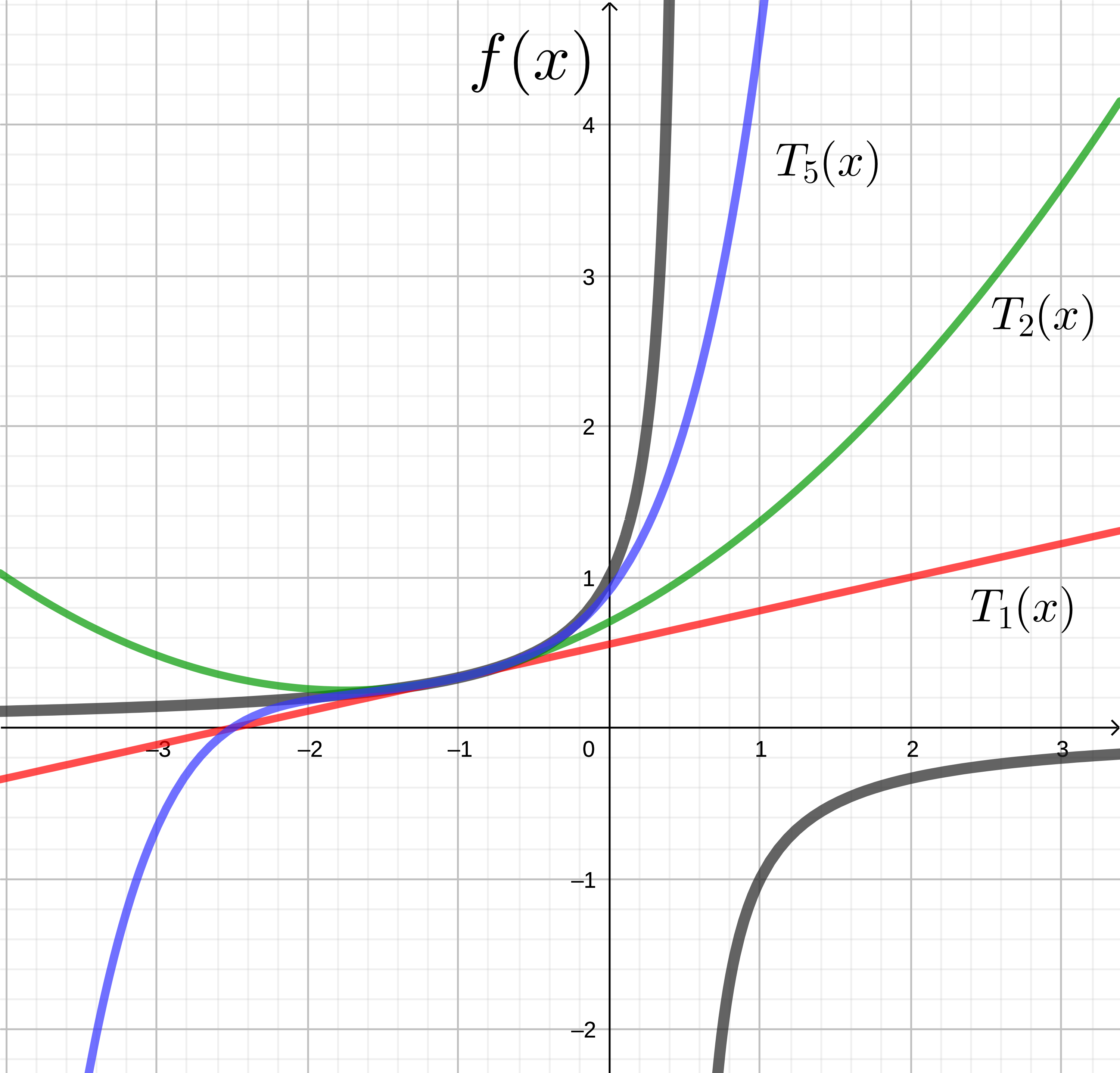
Taylor Polynomials#

Given a Taylor Series, we call each partial sum the Taylor Polynomial of degree n or \(T_n\). For instance:

\[\begin{split} T_1 (x) &= f(a)+f'(a)(x-a)\\[10pt] T_2 (x) &= f(a)+f'(a)(x-a)+\dfrac{f''(a)}{2!}(x-a)^2\\[10pt] T_3 (x) &= f(a)+f'(a)(x-a)+\dfrac{f''(a)}{2!}(x-a)^2+\dfrac{f'''(a)}{3!}(x-a)^3\\[10pt] \end{split}\]

Approximations

If function \(f\) has a power series representation centered at \(a\), then these Taylor Polynomials can be used to approximate the value of \(f(x)\).

For example: the \(T_1\) polynomial is the linear approximation.

Example 5#

Approximate the function \(f(x)=\dfrac{1}{1-2x}\) by a Taylor polynomial of degree 2 centered at \(a=-1\).

taylor-polynomial