(PE2) Eliminating the Parameter#
In this lesson we are going to see how to use the technique of eliminating the parameter to find a Cartesian equation to describe a parametric curve.
Review Videos#
Example 1#
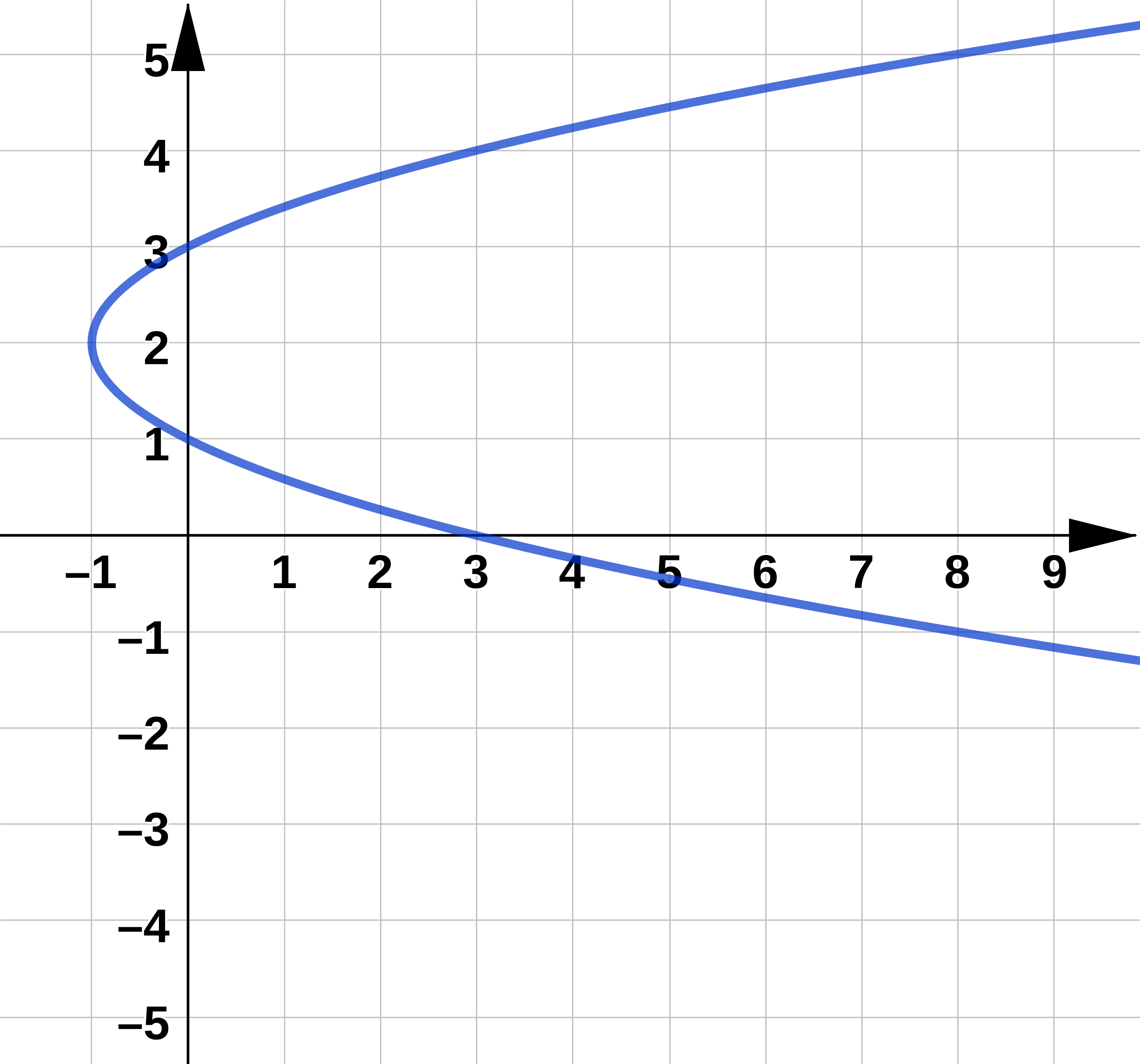
Eliminate the parameter to find a Cartesian equation of the parametric curve given by:
\[
x=t^2-2t\qquad \qquad y=t+1
\]
Example 2#
Eliminate the parameter to find a Cartesian equation of the parametric curve given by:
\[
x=\cos t\qquad y=\sin t \quad \text{with} \quad 0\leq t\leq 2\pi
\]
Example 3#
Eliminate the parameter to find a Cartesian equation of the parametric curve given by:
\[
x=\sin 2t\qquad y=\cos 2t \quad \text{with} \quad 0\leq t\leq 2\pi
\]
Parametric Curve vs Cartesian#
\[
x=\cos t\qquad y=\sin t \quad \text{with} \quad 0\leq t\leq 2\pi
\]
\[
x=\sin 2t\qquad y=\cos 2t \quad \text{with} \quad 0\leq t\leq 2\pi
\]
Example 4#
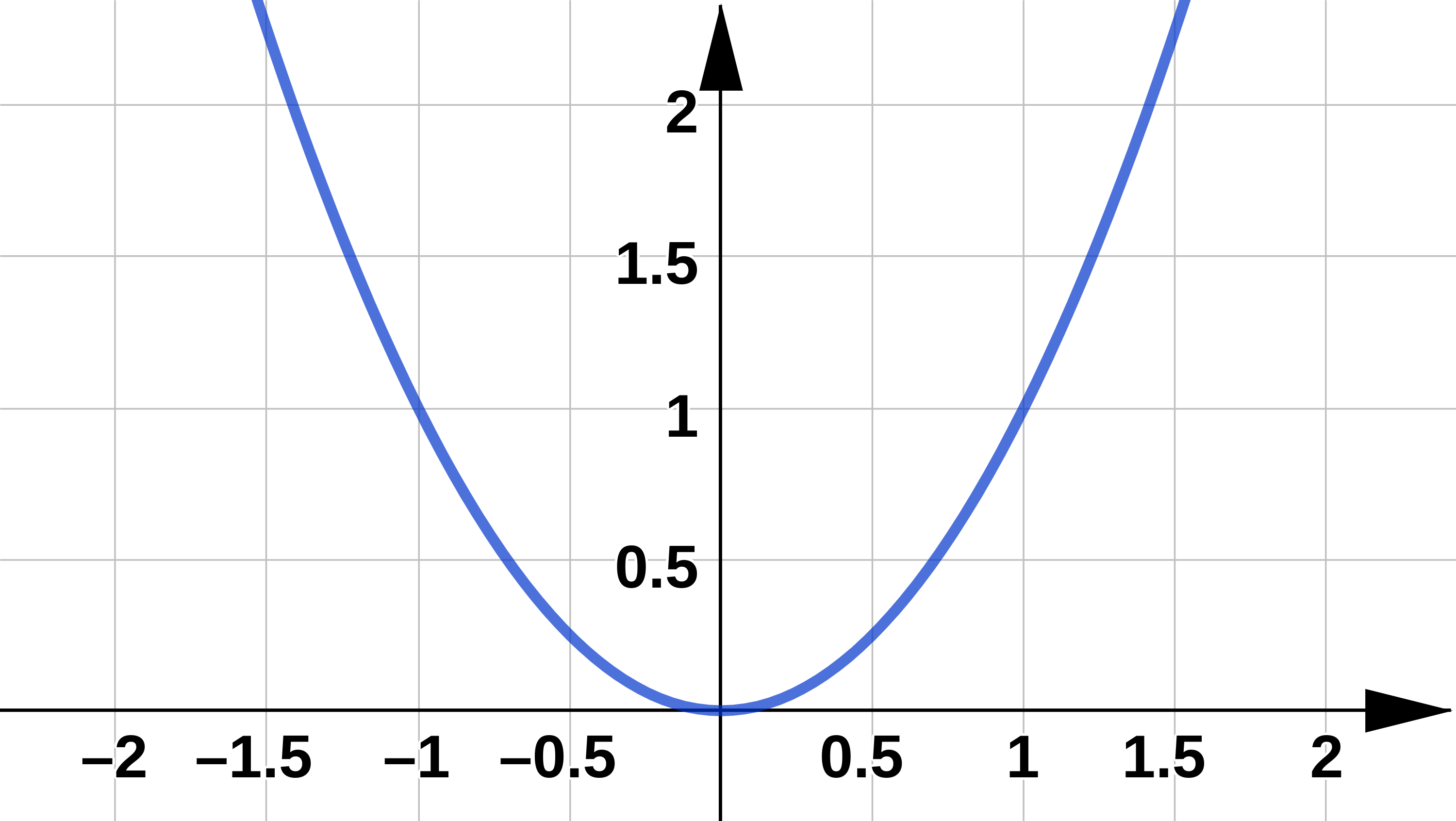
Eliminate the parameter to find a Cartesian equation of the parametric curve given by:
\[
x=\sin t\qquad y=\sin^2 t
\]
Common Parametric Curves#
Circle
\[
x=h+r\cos t \qquad \quad y=k + r\sin t \qquad \text{with} \quad 0\leq t\leq 2\pi
\]
Line Segment
\[
x=x_0+ t (x_1-x_0) \qquad \quad y=y_0+ t (y_1-y_0) \qquad \text{with} \quad 0\leq t\leq 1
\]
