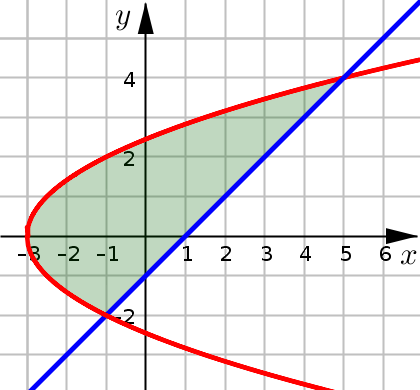
(AD1) Area Between Two Curves#

In this lesson we are going to see how to:

  • calculate the area of the region bounded between two curves.

Review Videos#

No review videos for this lesson.

Integral Formula#

Area Between Two Curves

The area of the region bounded by curves \(y=f(x)\) and \(y=g(x)\) and lines \(x=a\) and \(x=b\) is given by:

\[ \text{Area }= \int_a^b \bigg( f(x)- g(x) \bigg) \, dx \]

provided \(f(x)\geq g(x)\) on the interval \([a,b]\).

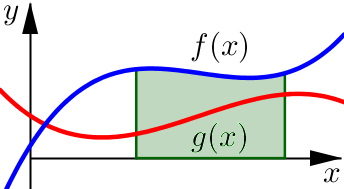
area01

area02

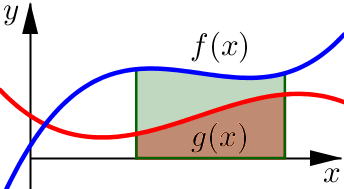
area03

area04

Strategy#

The Problem: Find the area of the region between two curves.

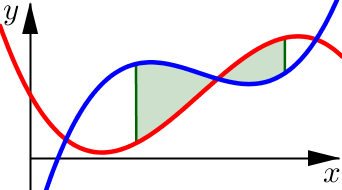
area05

The Strategy:

  1. Find the \(x\)-value(s) where the two functions intersect.

  2. Determine the interval(s) where \(f\) is above / below \(g\).

  3. Calculate the area over each interval.

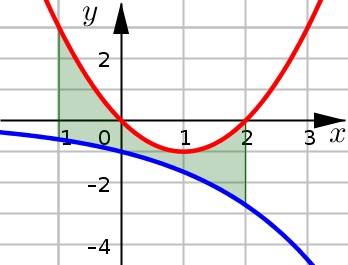
Example 1#

Find the area of the region:

  • bounded below by \(y=-e^{x/2}\)

  • bounded above by \(y=x^2-2x\)

  • bounded on the sides by \(x=-1\) and \(x=2\)

area1

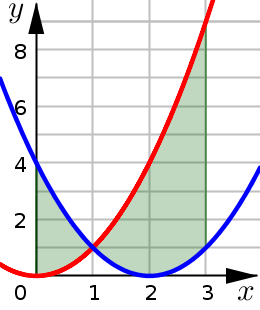
Example 2#

Find the area of the region from \(x=0\) to \(x=3\) bounded by curves:

\[ y=x^2 \qquad\text{and}\qquad y=x^2-4x+4 \]

area2

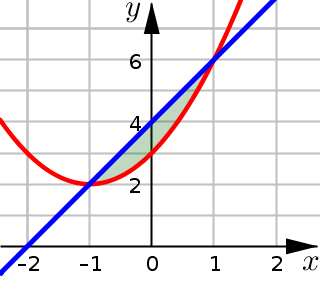
Example 3#

Find the area of the region bounded by the curves:

\[ y=x^2+2x+3 \qquad\text{and}\qquad y=2x+4 \]

area3

Example 4#

Find the area of the region bounded by curves:

\[ y=x-1 \qquad\text{and}\qquad y^2=2x+6 \]

area4