(PC1) Polar Coordinates#

In this lesson we are going to see:

  • how to plot points in the polar coordinate system.

  • how to convert between the Cartesian and polar coordinate representations for a point.

Review Videos#

Coordinate Systems#

A coordinate system gives us a way to describe a point in the plane with an ordered pair of numbers.

Cartesian Coordinate System

Origin is a point in the plane which we use to describe the relative location of all other points.

Coordinate Axes are the perpendicular axes intersecting at the origin and:

  • \(x\) measures the horizontal directed distance between the origin and point \(P\).

  • \(y\) measures the vertical directed distance between the origin and point \(P\).

Polar Coordinate System

Origin is a point in the plane which we use to describe the relative location of all other points.

Polar Axis is the ray starting at the origin usually corresponding to the positive \(x\) axis.

  • \(r\) is the total distance between point \(P\) and the origin.

  • \(\theta\) is the angle between the line \(OP\) and the polar axis.

Angle Conventions#

  1. Angle \(\theta\) is usually measured in radians.

  2. Positive \(\theta\) describes the angle in a counterclockwise direction around the origin.

  3. Negative \(\theta\) describes the angle in a clockwise direction around the origin.

Radius Conventions#

  1. If \(r=0\) then the point \(P(0,\theta)\) describes the origin for any \(\theta\)-value.

  2. The point \(P(-r,\theta)\) is the reflection of the point \((r,\theta)\) through the origin.

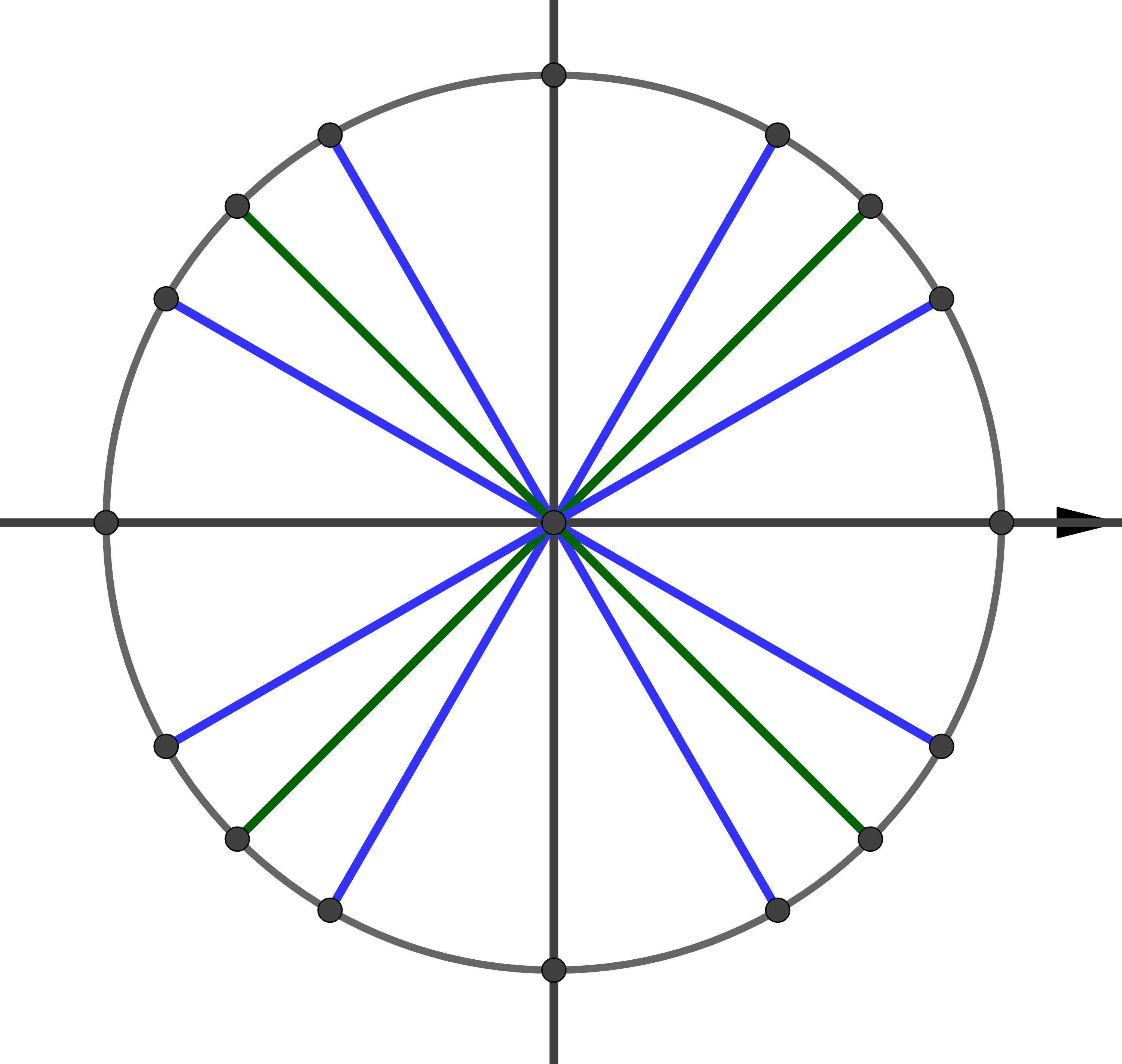
Important Angles#

The unit circle will prove to be a useful tool for identifying important angles and evaluating trigonometric functions. Let’s start by first identifying the angles:

\[ \theta = 0, \dfrac{\pi}{6}, \dfrac{\pi}{4}, \dfrac{\pi}{3}, \dfrac{\pi}{2}, \dots \]

Unit Circle

Example 1#

Plot the following points on the polar grid:

\[ \left(2,\dfrac{5\pi}{6} \right) \qquad \text{and}\qquad \left(3,\dfrac{5\pi}{2} \right) \]

Polar Grid

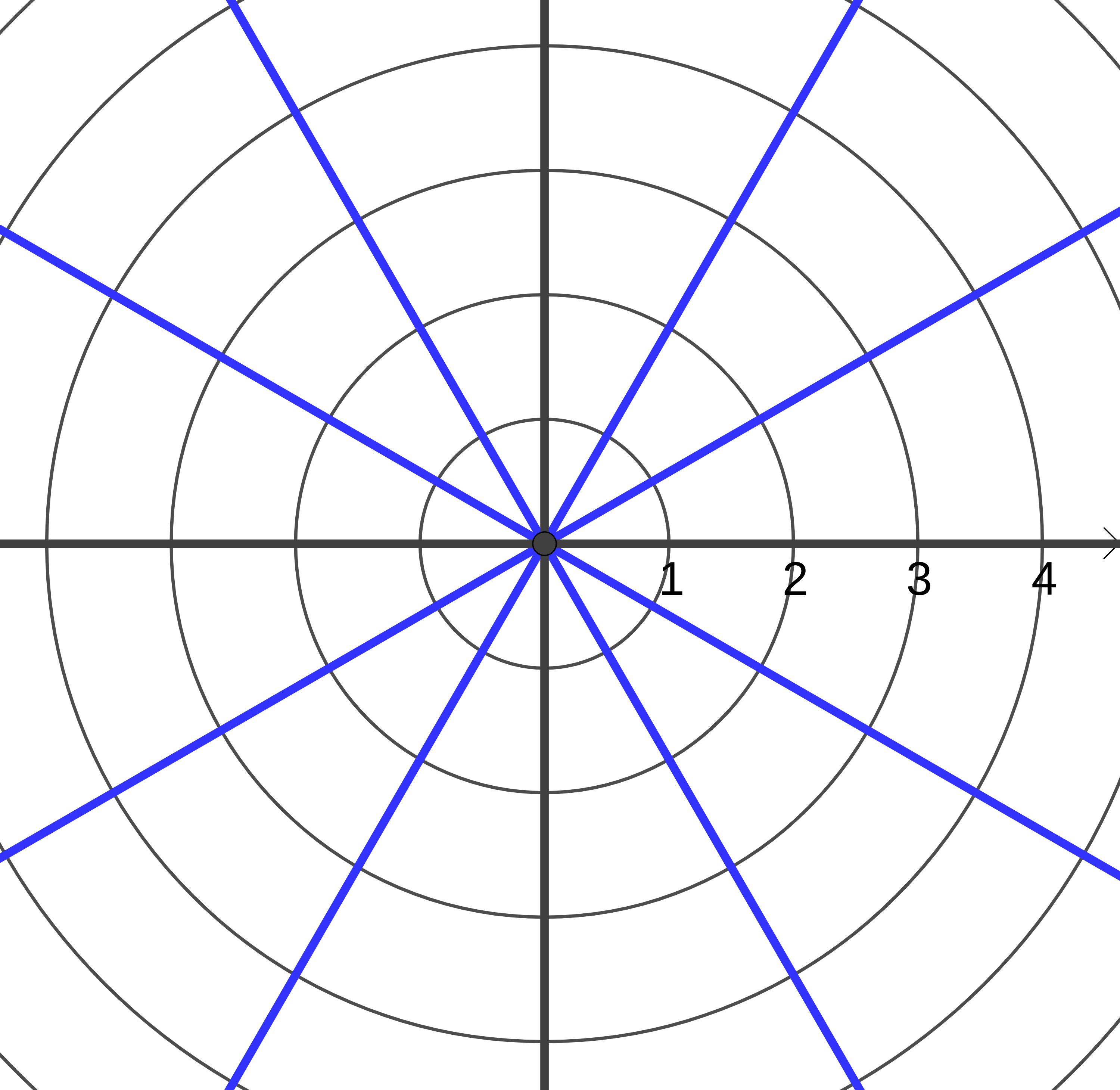
Example 2#

Plot the following points on the polar grid:

\[ \left(2,-\dfrac{3\pi}{4} \right) \qquad \text{and}\qquad \left(-4,\dfrac{2\pi}{3} \right) \]

Polar Grid

Multiple Representations#

Each point has an infinite amount of possible representations in the polar coordinate system.

\[ \big(r,\theta\big) \quad \qquad \big(r,\theta+2n\pi\big) \quad \qquad \big(-r,\theta+(2n+1)\pi\big) \]

In order to sidestep this issue, sometimes we choose to represent our points in a more standardized format with:

\[ r>0 \qquad \text{and} \qquad 0\leq \theta < 2\pi \]

Example 3#

Consider the point \(\left( 2, \tfrac{13\pi}{6}\right)\) given in polar coordinates.

  1. Find another pair of polar coordinates for this point such that \(r>0\) and \(0\leq \theta < 2 \pi\)

  2. Find another pair of polar coordinates for this point such that \(r<0\) and \(0\leq \theta < 2 \pi\)

Converting Between Coordinate Systems#

Polar to Cartesian

We know \((r,\theta)\) and need to find \(x\) and \(y\).

\[\begin{split} x&=r\cos\theta\\[10pt] y&=r\sin\theta\\[10pt] \end{split}\]
Cartesian to Polar

We know \((x,y)\) and need to find \(r\) and \(\theta\).

\[\begin{split} &r^2=x^2+y^2\\[10pt] &\tan\theta=\dfrac{y}{x}\\[10pt] \end{split}\]

Inverse Tangent Function#

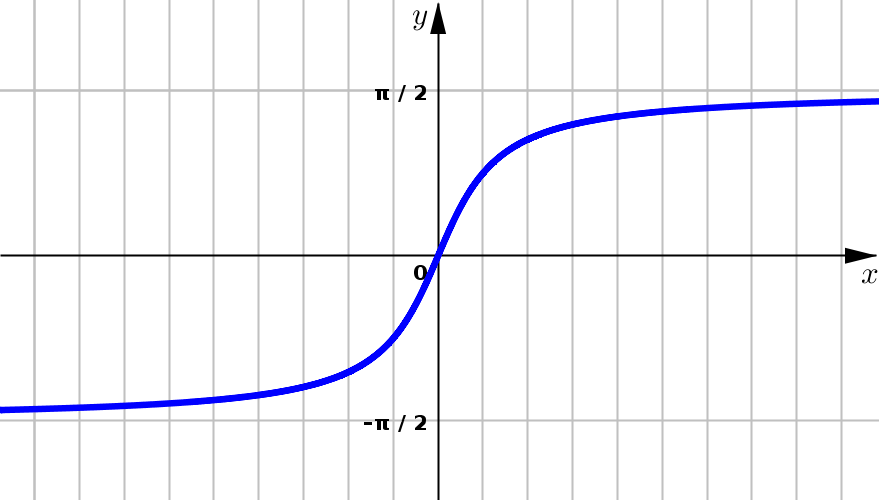
Inverse Tangent

We can use the inverse tangent function to help us find \(\theta\). However, by looking at the graph we see that \(\tan^{-1} w\) only takes on values in the interval \(\left(-\tfrac{\pi}{2},\tfrac{\pi}{2} \right)\). This means this function cannot be the only thing we use to find \(\theta\). Assuming we are choosing \(r\) so that \(r>0\), we can use values listed on the following table:

Location of point \((x,y)\)

\(0\leq \theta < 2\pi\)

\(-\pi< \theta \leq \pi\)

1st Quadrant

\(\theta = \tan^{-1} \left(\dfrac{y}{x}\right)\)

\(\theta = \tan^{-1} \left(\dfrac{y}{x}\right)\)

2nd Quadrant

\(\theta = \tan^{-1} \left(\dfrac{y}{x}\right)+ \pi\)

\(\theta = \tan^{-1} \left(\dfrac{y}{x}\right)+ \pi\)

3rd Quadrant

\(\theta = \tan^{-1} \left(\dfrac{y}{x}\right)+ \pi\)

\(\theta = \tan^{-1} \left(\dfrac{y}{x}\right)- \pi\)

4th Quadrant

\(\theta = \tan^{-1} \left(\dfrac{y}{x}\right)+ 2\pi\)

\(\theta = \tan^{-1} \left(\dfrac{y}{x}\right)\)

positive \(y\)-axis

\( \theta =\dfrac{\pi}{2}\)

\( \theta =\dfrac{\pi}{2}\)

negative \(y\)-axis

\( \theta =\dfrac{3\pi}{2}\)

\( \theta = -\dfrac{\pi}{2}\)

Example 4#

Convert the following points from polar into Cartesian coordinates.

\[ \left( 2, \tfrac{\pi}{6}\right) \qquad \text{and}\qquad \left( 4, \tfrac{-5\pi}{3}\right) \]

Example 5#

Convert the point \(\left( -2, -2\right)\) from Cartesian into polar coordinates.

Trigonometric Values#

The unit circle is also helpful for evaluating trigonometric functions at the important angles.

Unit Circle