(S1) Sequences#
In this lesson we are going to introduce the definition of a sequence, look at the different types of notation, and see how to visualize a sequence graphically.
By the end of this lesson, you will be able to:
write out the first few terms of a sequence given the general term \(a_n\).
Review Videos#
Definition of a Sequence#
Sequence
A sequence is a function with the set of positive integers as its domain.
We tend to think of a sequence as an infinite list:
where all of the terms of the sequence are written in a specific order. Relating this to function notation, we could also say \(f(n)=a_n\). Where the \(n\)th term of our sequence is equal to the function evaluated at number \(n\).
Notation#
We usually describe a sequence with a few different notations:
Writing out the first few terms:
Writing out the formula for the \(n\)th general term:
Example 1#
List the first four terms of the sequence:
(Click to see the steps.)
We notice that the \(n\)-values start with \(n=1\). To find the first four terms of the sequence, we will plug \(n=1\), \(n=2\), \(n=3\), and \(n=4\) into the formula of the general term:
Let’s calculate these:
Finally we write out the first four terms of our sequence:
Starting Index Value#
Starting Index Value
We can generalize the idea of sequences so that our index \(n\) starts at values other than \(n=1\).
Example 2#
List the first four terms of the sequence:
(Click to see the steps.)
We notice that the \(n\)-values start with \(n=3\). To find the first four terms of the sequence, we will plug \(n=3\), \(n=4\), \(n=5\), and \(n=6\) into the formula of the general term:
Let’s calculate these:
Finally we write out the first four terms of our sequence:
Factorials
Example 3#
List the first four terms of the sequence:
(Click to see the steps.)
We notice that the \(n\)-values start with \(n=0\). To find the first four terms of the sequence, we will plug \(n=0\), \(n=1\), \(n=2\), and \(n=3\) into the formula of the general term:
Let’s calculate these:
Finally we write out the first four terms of our sequence:
Example 4#
Find a formula for the general term \(a_n\) of the following sequence. Suppose that the sequence starts with index \(n=1\).
(Click to see the steps.)
We begin by noticing the alternating \(\quad - \quad + \quad - \quad + \quad \) pattern. How do we achieve this? Usually with either:
Since our index starts at \(n=1\), we see that only one of these works:
So we will use \((-1)^n\) in our final answer.
Next let’s look at the numerator. And to help with this let’s write out the index number that corresponds with each term:
Index |
1 |
2 |
3 |
4 |
|---|---|---|---|---|
Numerator |
\(3\) |
\(9\) |
\(27\) |
\(81\) |
To make this even more useful let’s try to factor each term in the numerator:
Index |
1 |
2 |
3 |
4 |
|---|---|---|---|---|
Numerator |
\(3\) |
\(3^2\) |
\(3^4\) |
\(3^4\) |
We see that in the:
first term we have one copy of \(3\)
second term we have two copies of \(3\)
third term we have three copies of \(3\)
So we conclude that the \(n\)th term would have \(n\) multiples of \(3\) or more specifically \(3^n\).
We also want to consider the denominator. Again, let’s write out the index number that corresponds with each term:
Index |
1 |
2 |
3 |
4 |
|---|---|---|---|---|
Denominator |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
We see that the denominator in the
first term is 3 more than index 1: \(\quad 4=3+1\)
second term is 3 more than index 2: \(\quad 5=3+2\)
third term is 3 more than index 3: \(\quad 6=3+3\)
So we conclude that the \(n\)th term would be 3 more than index \(n\) or more specifically: \(3+n\).
So far we have found that:
the \(-+-+\) pattern gives us \((-1)^n\)
the numerator would have \(3^n\)
the denominator would have \(n+3\).
Putting this all together, we get:
Graphical Representation#
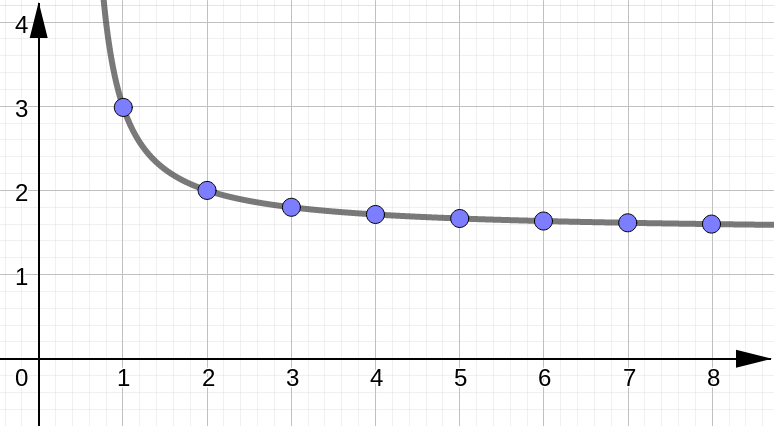
Sometimes it helps to have a visual depiction of a sequence.
Plot on the Cartesian Plane#
Plot the points \((n,a_n)\) on the usual \(xy\)-plane:
Plot on the Number Line#
Plot each term of the sequence \(a_n\) on the number line:

